Monty Haul Paradox

 Something ha s been bothering me about the Monty haul Paradox, and maybe I'm still wrong yet, I think I figured it out.

The Monty Haul Paradox - Paradox?

What is the Monty Haul Problem:

A Man at a Game Show is presented with 3 doors, behind one is a car, and behind the other 2 are goats. The contestant wants the car. He is instructed to pick a door. Once chosen the presenter opens a door and shows a goat, and then gives the contestant the chance to change. Should he.

The Average non mathematician will consider that the choice is 50/50 as there are now 2 doors, one with a goat, one with a car. 

Mathematicians though, insist that the chance is now 66.6% to swap. The reasoning is, the original theorem of the 3 doors. having one revealed when you had a 1/3rd chance, means statistically the door you have chosen was likely a goat. 

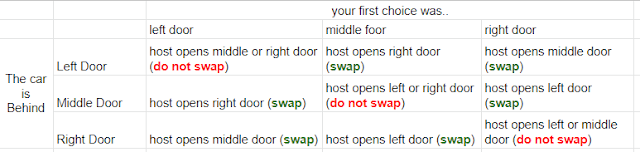
The graphs makes it 'clearer' there are 3 red end points, vs 6 green end points, so 6 of 9 choices or 2/3rds chance you'll be getting the car. right?

Now I can follow the logic of this, you can google it yourself to see the logic, and I guess its kinda makes more sense from that point of view, if you change it to 10 doors, where you choose 1 door, the presenter reveals 8 goats, and now you have 2 doors, do you want to change, but I spotted a flaw.

The Presenter, chose a goat door. of 2 possible goat doors, If you HAD chosen the car, he has 2 choices of goats to choose from, and if you had NOT chosen the car, he can only choose the 'other' goat.

Negating the presenters choice from the math, of course shows it to skew towards 66%, but if you spread out all choices with the presenter included, we return to 50/50.

In the chart above, we looked at 3 red vs 6 green. but forgot, that each red shows 2 choices. include them, and we're back to 6 vs 6 = 50/50. I don't have 3 dimensional excel to show it, so I need to split it out like this: